原文链接：2504.20073

简介

主要贡献：

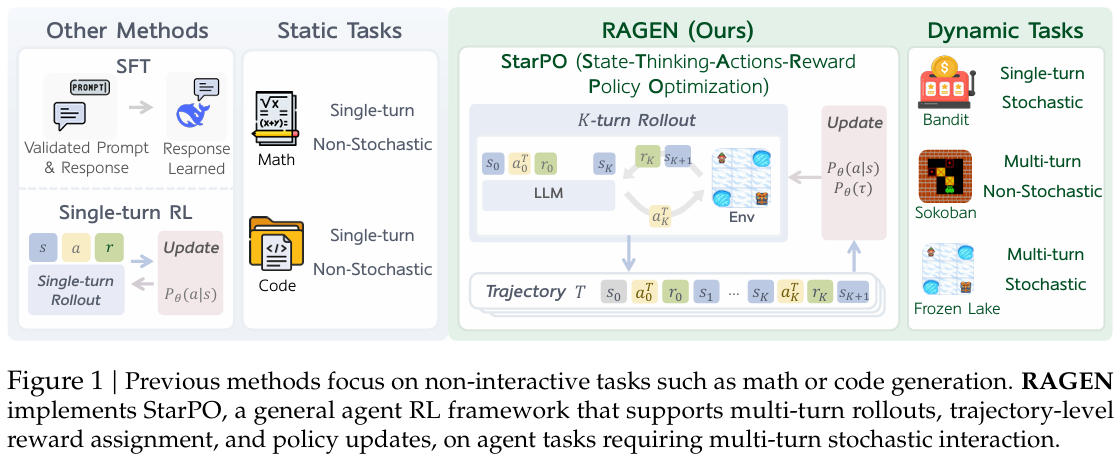
提出了 StarPO（State-Thinking-Actions-Reward Policy Optimization），一个多轮、轨迹级的智能体训练框架，能够灵活控制推理过程、奖励分配和prompt-rollout结构
开发了 RAGEN，一个用于训练和评估 LLM 智能体的模块化系统。
在三个特定环境：多臂老虎机(单轮，随机)、推箱子(多轮，确定性)和冰冻湖面(多轮，随机)的进行了实验，并揭示了三个核心发现。

核心发现：

多轮RL训练易出现不稳定。智能体过拟合局部奖励，表现为奖励方差崩溃、Rollout熵下降和梯度激增。该现象被作者称为 “回声陷阱(Echo Trap)”。
Rollout的频率和多样性非常重要。
- 确保进行Rollout的提示集内容足够多样，每个提示有多个响应
- 每轮执行多个动作，尽可能多探索；
- 保持较高的Rollout频率，确保执行Rollout的是最新策略。
智能体推理的出现需要细致的奖励信号。仅仅在格式上鼓励推理(例如使用 <think>的token）并不能保证推理的出现，如果推理没有明显的奖励优势，模型往往会回归到直接选择动作。猜测是因为任务中的动作空间简单，简单的策略就足够了。此外，当奖励仅反映任务成功时，模型推理时会产生幻觉。

方法

优化目标

先前的方法如PPO、GRPO，优化的是一个提示-响应对：

$$J_{step}(\theta)=\mathbb{E}_{x\sim\mathcal{D},y\sim\pi_{\theta}(\cdot|x)}[R(x,y)]$$

而本文的方法则是优化整条轨迹的总奖励：

$$J_{\mathrm{StarPO}}(\theta)=\mathbb{E}_{\mathcal{M},\tau\sim\pi_{\theta}}\left[R(\tau)\right]$$

优化过程

在每次训练迭代中，智能体从初始状态$s_0$开始生成$N$个轨迹。在每个步骤$t$，智能体产生一个由推理引导的结构化输出：
$a_t^T$=<think>…<think><answer>$a_t$<answer>
其中$a_t^{T}$是包括中间推理过程的完整行动输出，$a_t$是是包括中间推理过程的完整行动输出，然后环境返回下一个状态$s_{t+1}$和奖励$r_t$。
Rollout阶段产生完整的轨迹形如：$\tau=s_0,a_0^T,r_0,s_1,...,a_{K-1}^T,r_{K-1},s_K$。
StarPO 交替进行Rollout和学习。

Rollout可以采用当前策略$\pi_{\theta}$进行采样，也可以从旧策略$\pi_{old}$的Replay Buffer中采样。
训练循环$L$次，每个循环内包含$P$个初始状态，每个初始状态产生$N$条轨迹，batch size为$E$，因此共产生$S={\frac{L\cdot P\cdot N}{E}}$次梯度更新。

优化策略

StarPO 在统一的轨迹级抽象下支持多种策略优化算法。对于轨迹$\tau_{i}$，使用以下token级更新的优化策略实例化 StarPO：
PPO

$$J_{\mathrm{PPO}}(\theta)=\frac{1}{G}\sum_{i=1}^{G}\frac{1}{|\tau_{i}|}\sum_{t=1}^{|\tau_{\mathrm{i}}|}\min\left[\frac{\pi_{\theta}(\tau_{i,(t)}|\tau_{i,\mathrel{<}t})}{\pi_{\mathrm{old}}(\tau_{i,(t)}|\tau_{i,\mathrel{<}t})}\cdot A_{i,t},\mathrm{clip}\left(\frac{\pi_{\theta}(\tau_{i,(t)}|\tau_{i,\mathrel{<}t})}{\pi_{\mathrm{old}}(\tau_{i,(t)}|\tau_{i,\mathrel{<}t})},1-\varepsilon,1+\varepsilon\right)\cdot A_{i,t}\right]$$

其中$G$是批次中的轨迹数量，$|\tau_i|$为轨迹$\tau_i$的长度，$\tau_{i,(t)}$示轨迹$\tau_{i}$中的第$t$个token，$\tau_{i,\mathrel{<}t}$ 是前$t$个token。
GRPO
在GRPO中，每个轨迹分配一个奖励$R_{\tau}$，并在批次中对其进行归一化。轨迹中所有的token均采用该归一化奖励作为优势值

$$\hat{A}_{i,t}=\frac{R(\tau_i)-\max(\{R(\tau_1),\ldots,R(\tau_G)\})}{\operatorname{std}(\{R(\tau_1),\ldots,R(\tau_G)\})}$$

$$J_{\mathrm{GRPO}}(\theta)=\frac{1}{G}\sum_{i=1}^{G}\frac{1}{|\tau_{i}|}\sum_{t=1}^{|\tau_{i}|}\min\left[\frac{\pi_{\theta}(\tau_{i,(t)}|\tau_{i,\mathrel{<}t})}{\pi_{\mathrm{old}}(\tau_{i,(t)}|\tau_{i,\mathrel{<}t})}\cdot\hat{A}_{i,t},\mathrm{clip}\left(\frac{\pi_{\theta}(\tau_{i,(t)}|\tau_{i,\mathrel{<}t})}{\pi_{\mathrm{old}}(\tau_{i,(t)}|\tau_{i,\mathrel{<}t})},1-\varepsilon,1+\varepsilon\right)\cdot\hat{A}_{i,t}\right]$$

实验

实验设置

环境与任务

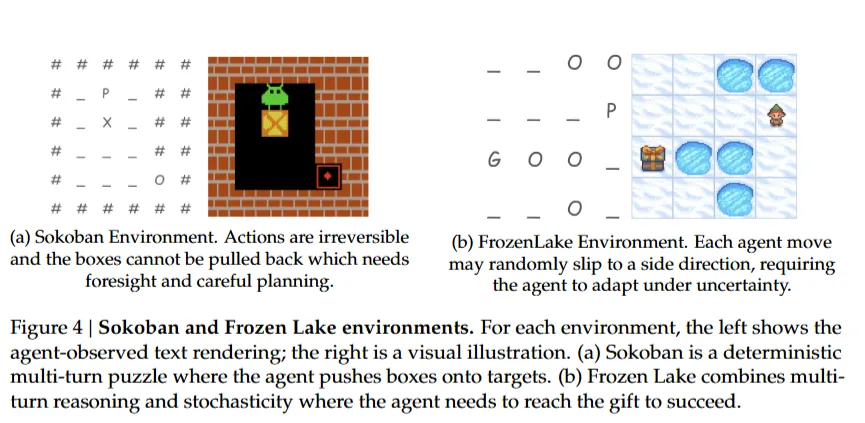
多臂老虎机(单轮，随机)
推箱子(多轮，确定性)
冰冻湖面(多轮，随机)

训练设置

显卡：单张H100 GPU
模型：Qwen-2.5-0.5B
数据参数：

Rollout次数$L$：200（总的训练轮数）
采样Batch大小$P$：8 （一个batch内$s_0$的数量）
每个提示采样轨迹数$N$：16
最多进行5轮环境交互、执行10 次动作(每轮交互可能不止执行一次动作)
更新Batch大小$E$：32
单GPU的Micro Batch大小：4
训练参数
GAE的$\gamma$：1.0
GAE的$\lambda$：1.0
熵正则系数$\beta$：0.001
格式奖励：-0.1

评估指标

在每个环境中对 256 个固定提示进行评估，温度$T$=0.5，并在 5 轮后截断episode。评估指标包括：

成功率（任务完成情况）
rollout熵（探索程度）：计算响应在token层面的平均熵值，用于捕捉探索程度与策略不确定性。熵值骤降可能预示策略过早收敛或崩溃。
组内奖励方差（行为多样性）：高组内方差反映行为多样性与学习潜力；突然坍缩则表明奖励同质化与策略停滞。
响应长度（推理的详细程度）
梯度范数（训练稳定性）
所有指标均基于在线策略Rollout计算，并经过 EMA 平滑处理。

实验结果与发现

现象1：训练不稳定

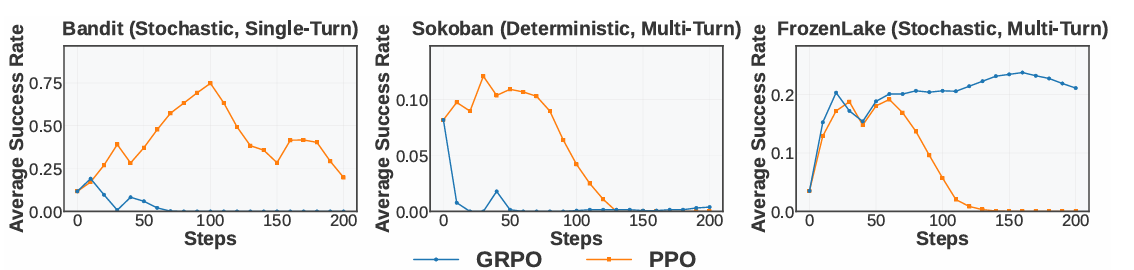
早期轨迹具有多样性，但后期则变得重复和确定。这种失败模式被作者称为“Echo Trap”。

作者研究了Echo Trap发生时伴随的指标变化：奖励标准差和Rollout熵变小、平均奖励停滞或下降、梯度范数激增。
如下图所示，奖励标准差和熵提前下降，通常在奖励降低之前，可以作为早期预警信号。奖励均值和梯度范数直接反映崩溃。

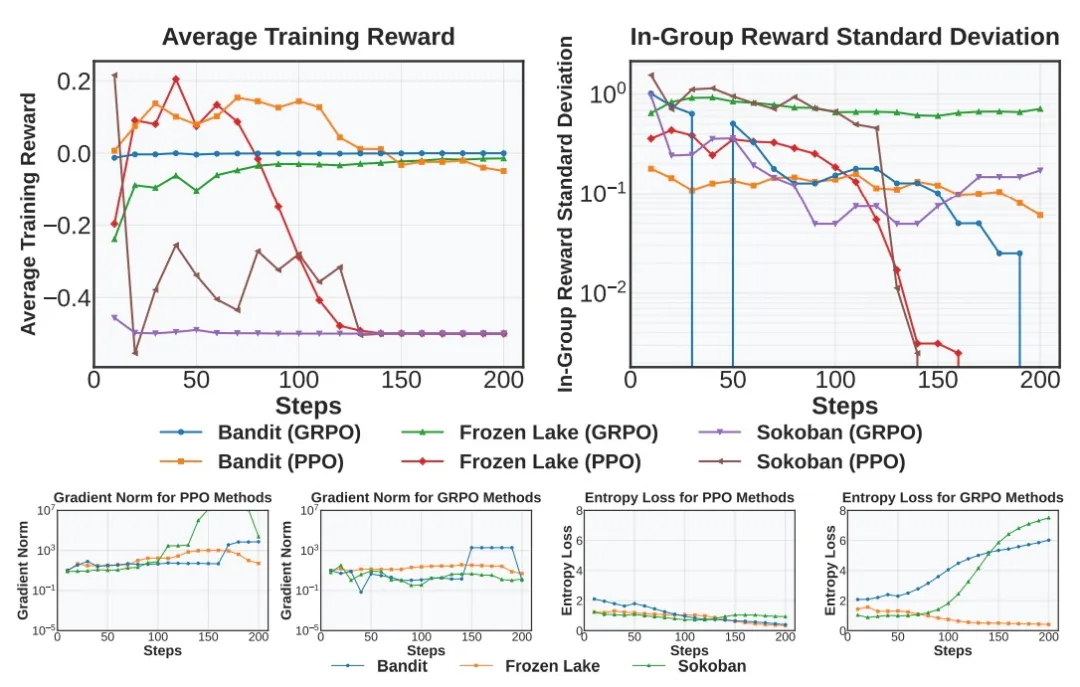
针对现象1，本文采取了技巧1和技巧2提升训练稳定性。

技巧1：过滤低方差轨迹

StarPO-S是StarPO的稳定版变体，做了如下修改：
过滤低方差样本。每次Rollout后计算轨迹的奖励标准差，训练时仅保留排名靠前的提示。保留比例的影响如下图：

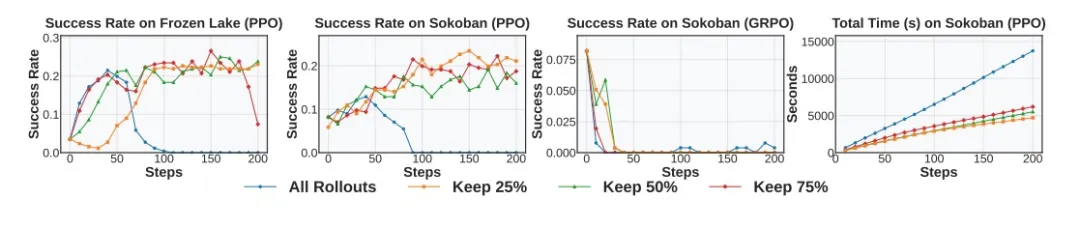除此之外还加入了DAPO中的trick：

KL项的移除：鼓励模型探索
Clip-Higher：允许模型从高回报的Rollout中更积极地学习

技巧2：提高轨迹质量

从上文看得出轨迹质量非常重要，那哪些因素可以衡量轨迹的质量呢？作者通过实验确定了三个维度：任务多样性、交互粒度和Rollout频率。

任务多样性是指训练期间使用的不同初始状态的数量。
交互粒度指的是每条轨迹中允许的动作数量。
Rollout频率衡量的是每多少次更新后再进行一次采样。
针对任务多样性，作者通过在保持batch size不变的情况下，改变单个提示对应的响应数量来修改任务多样性。任务多样性与每个提示的响应数量成反比)。实验中发现每个prompt产生4个响应的效果最佳。

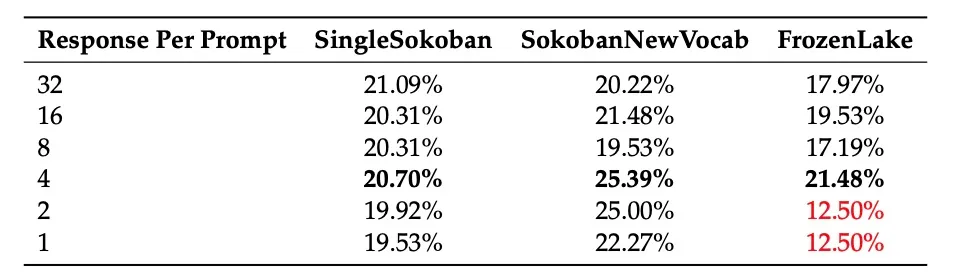
针对交互粒度，作者发现每回合允许 5-6 个作可以持续提高成功率，同时避免过长的Rollout带来的噪音。
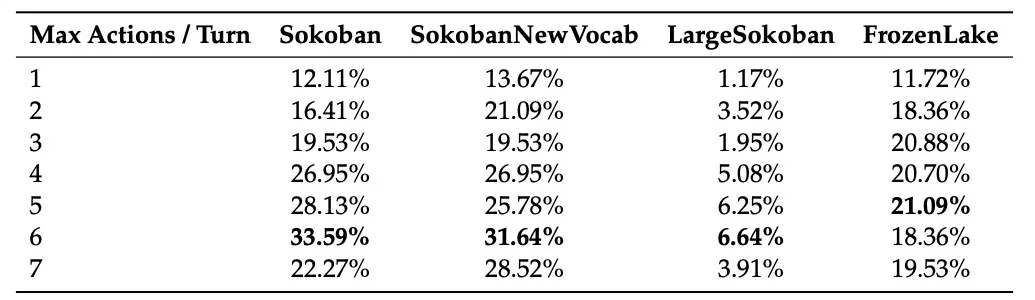针对Rollout频率，作者发现Rollout频率越高训练越稳定。图中Online K指的是一组Rollout将重复用于K次连续的策略更新，K越小Rollout频率越高。

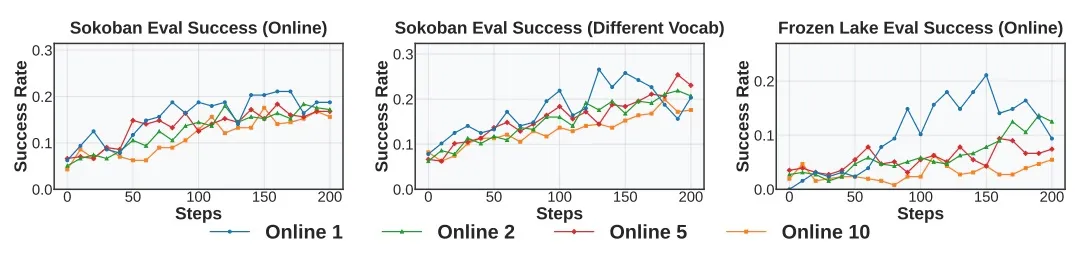
现象2：推理输出逐渐消失

作者发现，推理显著提高了 Bandit 等单轮任务中的泛化，但在 Sokoban 等更复杂的多步骤环境中无法增长或持续存在。在多轮次任务中，推理信号会随着训练的进行而减弱，最终模型会倾向于直接输出action。

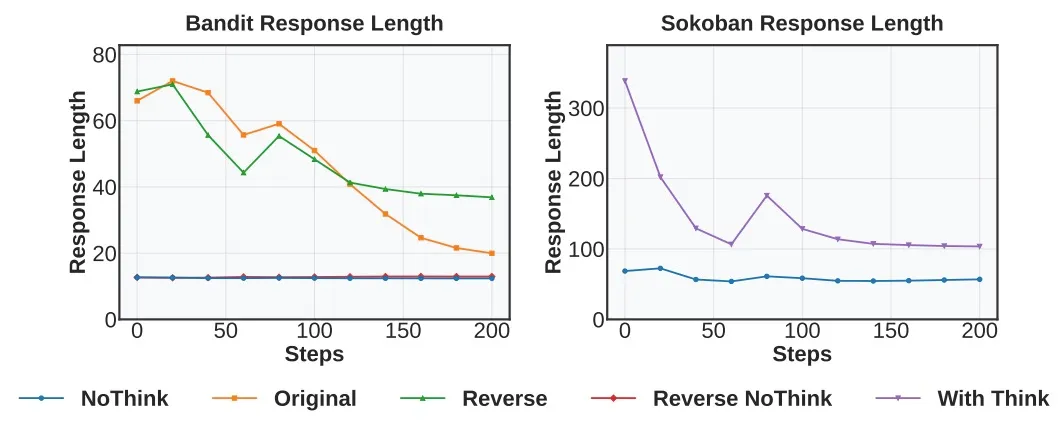
直接删除推理的变体在非Bandit环境中表现的也更好。

技巧3：增加细致的奖励

针对现象2，作者猜测多轮次任务中的奖励信号可能太嘈杂，无法可靠地支持细粒度推理学习。在这样的环境中，奖励信号通常是稀疏的、延迟的和基于结果的，这使得很难区分由推理得到的成功轨迹和通过试错实现的成功轨迹。作者还观察到模型产生不连贯的甚至幻觉的推理但仍能得出正确答案的例子。
因此，作者认为单靠奖励是无法反映推理的质量的，一种可行的方法是将动作的正确性与推理质量分离。为此，作者采用了基于格式的惩罚：当模型无法产生有效的 <think>–<answer> 结构时，即使最终的答案是正确的也给予负奖励。

局限性

模型方面， RAGEN 尚未在多模态模型或更大的模型上进行评估。
奖励方面， RAGEN 尚未针对奖励难验证的环境进行优化。
3. 长上下文问题：多轮交互产生的长上下文会导致 KV 缓存占用过大，这限制了 RAGEN 在更长、更复杂任务上的训练效率。

参考

RAGEN：通过多轮RL强化学习理解 LLM Agent的自我进化