原文链接:Curiosity-driven Exploration by Self-supervised Prediction
简介
问题提出:现实场景外部奖励少,需要内部奖励
关键贡献:
- 将好奇心定义为智能体在智能体在视觉特征空间中预测自身行为后果的能力所产生的误差,而该视觉特征空间是由自监督逆动力学模型(self-supervised inverse dynamics mode)学习而得到的。该定义适用于像图像这样的高维连续状态空间,避开了直接预测像素这个难题的同时忽略了环境中那些对智能体没有影响的因素。
- 在两个环境中评估了所提出的方法:VizDoom 和超级马里奥兄弟(Super Mario Bros)。
- 研究了三种主要的场景:
- 稀疏的外部奖励场景,在这种情况下,好奇心能让智能体通过与环境进行更少的交互来达成目标;
- 无外部奖励的探索场景,好奇心促使智能体更高效地进行探索;
- 对未见场景(例如同一游戏的新关卡)的泛化场景,在这种场景中,从先前经验中获得的知识能帮助智能体比从头开始探索新地方的速度快得多。
方法
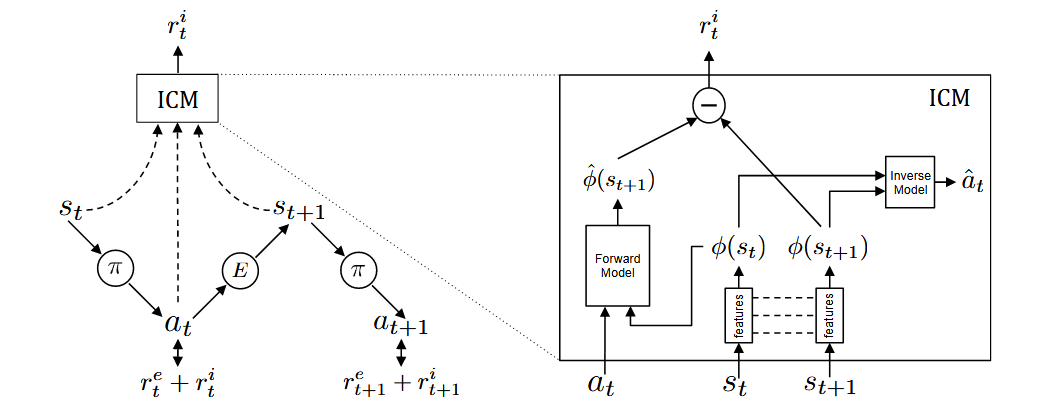
整个框架由两个网络组成,策略网络和ICM(Intrisic Curiosity Module,内在好奇心模块)。
策略网络训练
策略网络$\theta_{P}$的训练如左图所示,处于状态$s_{t}$的智能体通过执行从当前策略$\pi$中采样得到的动作$a_{t}$与环境进行交互,并最终到达状态$s_{t+1}$,策略$\pi$通过优化环境$E$提供的外部奖励$r_{t}^{e}$与我们提出的内在好奇心模块(ICM)生成的基于好奇心的内在奖励信号$r_{t}^{i}$之和进行训练,即通过最大化期望奖励之和来优化$\theta_{P}$:
$\max_{\theta_{P}}\mathbb{E}_{\pi(s_{t};\theta_{P})}\left[\sum_{t}r_{t}\right]$
ICM训练
ICM则由两个模型组成,前向模型(Forward Model)和逆向模型(Inverse Model)。
逆向模型训练
逆向模型首先将原始状态$s_{t}$和$s_{t+1}$通过features网络编码为特征向量$\phi(s_{t})$和$\phi(s_{t+1})$,然后将$\phi(s_{t})$、$\phi(s_{t+1})$作为输入,预测智能体从状态$s_{t}$转移到$s_{t+1}$所采取的动作$\hat{a}_{t}$,网络参数$\theta_{I}$则通过优化以下式子进行训练:
$\min_{\theta_{I}}L_{I}(\hat{a}_{t},a_{t})$
其中,$L_{I}$是衡量预测动作和实际动作差异的损失函数。这部分就是简介中提到的逆动力学模型。
前向模型训练
前向模型将$a_{t}$和$\phi(s_{t})$作为输入,并预测$t + 1$时刻状态的特征编码$\hat{\phi}(s_{t+1})$,网络参数$\theta_{F}$通过最小化损失函数$L_{F}$进行优化:
$L_{F}(\phi(s_{t}),\hat{\phi}(s_{t+1}))=\frac{1}{2}\left\|\hat{\phi}(s_{t+1})-\phi(s_{t+1})\right\|_{2}^{2}$
内在奖励计算
内在奖励信号$r_{t}^{i}$计算如下:
$r_{t}^{i}=\frac{\eta}{2}\left\|\hat{\phi}(s_{t+1})-\phi(s_{t+1})\right\|_{2}^{2}$
其中$\eta>0$是一个缩放因子。这个内在奖励就是好奇心。
ICM设计理念
简单来说,ICM通过两个相邻的状态以及之间的动作来计算内在奖励,即把状态预测误差作为好奇心。这就是为什么要引入前向模型:用于预测状态。那为什么要引入逆向模型呢?这是因为ICM的作者认为,状态三部分信息。
- 可以被智能体控制的部分;
- 不能被智能体控制但是可以影响智能体的部分;
- 既不能被控制也不能影响智能体的部分(例如游戏画面的背景是树叶在舞动) 一个好的表示应该包含前两项的信息,而不包含后两项的信息。因此作者设计反向模型,让反向模型去预测动作,让反向模型学会辨别状态中的哪些特征是被动作影响的,从而获得最合理的状态特征。
训练细节
- 输入的RGB图像被转换为灰度图并调整大小为42×42,状态$s_{t}$为当前帧与三帧的拼接
- 训练时VizDoom每四帧采样一次动作,马里奥每六帧。测试时则每帧都采样。
- 策略采用A3C。A3C模型采用四个卷积层的卷积网络+LSTM+全连接
- ICM的逆向模型采用四个卷积层将输入状态($s_{t}$)映射到特征向量$\phi(s_{t})$,接着拼接$\phi(s_{t})$和$\phi(s_{t+1})$输入到全连接层。前向模型则是一个全连接网络。
- 最终的训练目标是三个网络一起训练 $\min_{\theta_{P},\theta_{I},\theta_{F}}\left[-\lambda\mathbb{E}_{\pi(s_{t};\theta_{P})}\left[\sum_{t}r_{t}\right]+(1 - \beta)L_{I}+\beta L_{F}\right]$