原文链接：#Exploration:A Study of Count-Based Explorationfor Deep Reinforcement Learning

简介

当前深度 RL 探索策略虽能处理高维连续空间，却依赖复杂启发式方法。本文旨在探索简单的经典计数方法推广至高维空间的可行性，提出了一种基于哈希的计数探索方法。

核心问题与挑战

经典计数探索的局限性：传统方法（如MBIE-EB）依赖状态-动作对的精确计数，仅适用于低维离散状态空间。高维连续空间中，大多数状态仅出现一次，直接计数无效。
现有方法的不足
- 内在激励（如VIME、伪计数）需要复杂密度模型或动力学模型，计算成本高。
- 基于不确定性的方法（如Bootstrapped DQN）依赖集成或贝叶斯框架，实现复杂。

方法

基于静态哈希的计数探索(Count-Based Exploration via Static Hashing)

核心思想

通过哈希函数 $\phi: \mathcal{S} \rightarrow \mathbb{Z}$ 将连续高维状态空间离散化为哈希码，利用哈希表记录状态访问次数 $n(\phi(s))$，并计算探索奖励：

$$ r^+(s) = \frac{\beta}{\sqrt{n(\phi(s))}}, $$

其中 $\beta$ 是奖励系数。初始时所有状态计数 $n(\cdot)$ 为 0，每次遇到状态 $s_t$ 时更新 $n(\phi(s_t)) \leftarrow n(\phi(s_t)) + 1$。训练时使用总奖励 $r + r^+$，但评估时仅用原始奖励 $r$。

关键点

状态计数 vs. 状态-动作计数：论文发现仅计数状态（而非状态-动作对）已足够，因为策略本身具有随机性，能在新状态尝试多种动作。
哈希函数的选择：哈希函数需平衡“粒度”与“泛化能力”：
- 粒度：相似状态应映射到相同哈希码，不相似状态应区分。
- 先验知识：可通过设计哈希函数编码与任务相关的状态特征。

实现方法

SimHash：一种高效的局部敏感哈希（LSH），基于角度距离生成二进制哈希码：
$$ \phi(s) = \text{sgn}(A g(s)) \in \{-1, 1\}^k, $$
其中 $g: \mathcal{S} \rightarrow \mathbb{R}^D$ 是预处理函数（如归一化），$A$ 是 $k \times D$ 的高斯随机矩阵。参数 $k$ 控制粒度，值越大区分能力越强。

基于学习哈希的计数探索（Count-Based Exploration via Learned Hashing）

动机

对于复杂状态（如图像），直接使用像素空间的SimHash可能无法捕捉语义相似性。因此，论文提出用自编码器（AE）学习更有意义的哈希码。

自编码器设计

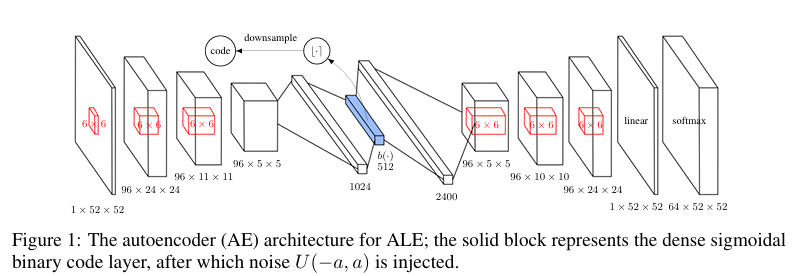
结构：
- 输入：状态 $s$（如图像）。
- 特殊层：一个包含 $D$ 个sigmoid单元的稠密层，输出 $b(s) \in [0,1]^D$。
- 二值化：对 $b(s)$ 四舍五入得到二进制码 $\lfloor b(s) \rceil \in \{0,1\}^D$。
噪声注入：在sigmoid激活后加入均匀噪声 $U(-a, a)$（$a > \frac{1}{4}$），迫使AE将相似状态的编码分散开以抵抗噪声干扰。
损失函数：

$$ L(\{s_n\}) = -\frac{1}{N} \sum_{n=1}^N \left[ \log p(s_n) - \frac{\lambda}{D} \sum_{i=1}^D \min \{(1-b_i(s_n))^2, b_i(s_n)^2\} \right], $$
- 第一项：负对数似然（重构误差）。
- 第二项：迫使二进制码接近0或1（通过$\lambda$加权）。
降维：由于学习到的二进制码维度较高，需通过SimHash进一步降维。

训练细节

稳定性：通过降低学习率或减少二进制码维度保持哈希函数一致性。
饱和行为：sigmoid单元对已学习状态饱和，减少梯度更新对编码的影响。

算法流程

静态哈希（Algorithm 1）

初始化哈希表 $n(\cdot)$ 和哈希函数 $\phi$。
对于每个时间步 $t$：
- 观察状态 $s_t$，计算哈希码 $\phi(s_t)$。
- 更新计数 $n(\phi(s_t)) \leftarrow n(\phi(s_t)) + 1$。
- 计算探索奖励 $r^+(s_t) = \beta / \sqrt{n(\phi(s_t))}$。
- 执行动作 $a_t \sim \pi(\cdot|s_t)$，环境返回 $r_t$。
- 使用 $r_t + r^+(s_t)$ 更新策略。

学习哈希（Algorithm 2）

初始化自编码器和哈希表。
定期用最新数据更新自编码器，生成二进制码并降维。
其余步骤与静态哈希相同。

哈希函数的关键特性

适当粒度：
- 低粒度（如 $k=16$）：哈希码过少，无法区分关键状态。
- 高粒度（如 $k=512$）：过度区分琐碎细节，导致探索效率下降。
编码相关信息：
- 哈希函数应编码与解决MDP相关的状态特征（如目标位置、敌人在蒙特祖玛的复仇中的位置）。
- 实验显示，忽略无关特征（如敌人位置）可能提升性能。

技术细节与优化

计数数据结构：使用计数布鲁姆过滤器（Counting Bloom Filter）或Count-Min Sketch减少内存开销，通过多个哈希函数降低冲突概率。
超参数选择：
- $\beta$：需随哈希粒度调整（高粒度需小$\beta$避免奖励淹没）。
- $k$：通过网格搜索确定（如Atari实验中 $k=256$）。

总结

论文方法的核心是通过哈希将高维状态离散化，利用计数奖励鼓励探索。其优势在于：

简单高效：无需复杂密度模型，计算开销低。
灵活性：支持静态哈希（SimHash）和学习哈希（AE），适应不同任务。
通用性：在连续控制（如MountainCar）和图像任务（如Atari）中均表现优异。

实验部分验证了哈希函数的设计对性能的关键影响，并展示了该方法在稀疏奖励任务中的有效性。

Hash-based Counts

#Exploration: A Study of Count-Based Exploration for Deep Reinforcement Learning

简介