原文地址:1507.00814
简介
为了解决探索问题,先前的研究提出了“不确定性下乐观”的方法。如果假设强化学习算法倾向于选择最佳动作,那么可以通过增加奖励函数来鼓励它访问不常出现的状态-动作对,从而获得探索奖励。这通过增广奖励函数实现:
$R_{Bonus}(s, a) = R(s, a) + \beta N(s, a)$ (1)
其中 $N(s, a): S \times A \to$ 是一个新奇性函数(novelty function),旨在捕获给定状态-动作对的新奇性。先前的研究提出了各种基于状态访问频率的新奇性函数。然而,这些方法需要对智能体的状态-动作空间进行简洁的、通常是离散的表示,以测量状态访问频率。
本文的方法则采用函数逼近和表示学习来规避这些限制。
方法
模型学习与探索奖励
令 $\sigma(s)$ 表示状态 $s$ 的编码,令 $M_\phi: \sigma(S) \times A \to \sigma(S)$ 是一个由 $\phi$ 参数化的动力学模型。$M_\phi$ 接收状态 $s$ 在时间 $t$ 的编码版本 $\sigma(s_t)$ 和智能体在时间 $t$ 的动作 $a_t$,并尝试预测智能体在时间 $t+1$ 的状态编码版本 $\sigma(s_{t+1})$。
对于每个状态转移 $(s_t, a_t, s_{t+1})$,可以尝试使用预测模型 $M_\phi$ 从 $(\sigma(s_t), a_t)$ 预测 $\sigma(s_{t+1})$。这个预测会存在一些误差:
$e(s_t, a_t) = |\sigma(s_{t+1}) - M_\phi(\sigma(s_t), a_t)|_2^2$ (2)
令 $e_T$ 为时间 $T$ 的标准化预测误差,其定义为 $e_T := e_T / \max_{t \le T} {e_t}$。则新奇性函数可以写成
$N(s_t, a_t) = \frac{\bar{e}_t(s_t, a_t)}{t * C}$ (3)
其中 $C > 0$ 是一个衰减常数。现在,增广奖励函数可以表示为:
$R_{Bonus}(s, a) = R(s, a) + \beta \left( \frac{\bar{e}_t(s_t, a_t)}{t * C} \right)$ (4)
这种方法的核心思想是,随着模型对特定状态-动作对动力学建模能力的提高,对其的理解也越深入,因此其新奇性越低。反之,当对某个状态-动作对的理解不足以进行准确预测时,会分配更高的新奇性。
使用学习到的动力学模型来分配新奇性函数,使得我们能够以非贪婪的方式解决探索与利用问题。只要遇到足够多的相似状态-动作对,即使遇到新的状态-动作对 $(s_t, a_t)$,我们仍然期望 $M_\phi(\sigma(s_t), a_t)$ 的预测是准确的。
本文的模型化探索奖励可以集成到任何基于状态、动作、奖励元组 $(s_t, a_t, s_{t+1}, r_t)$ 更新策略的在线强化学习算法中,例如Q-learning或Actor-Critic算法。该方法总结在算法1中:
算法1 带有模型预测探索奖励的强化学习

在每个步骤中,算法接收元组 $(s_t, a_t, s_{t+1}, R(s_t, a_t))$,并计算编码状态 $\sigma(s_{t+1})$ 与模型 $M_\phi(\sigma(s_t), a_t)$ 预测之间的欧几里得距离。这个距离用于根据公式 (4) 计算增广探索奖励 $R_{Bonus}$。元组 $(s_t, a_t, s_{t+1}, R_{Bonus})$ 在每个步骤结束时存储在记忆库 $\Omega$ 中。策略在每一步都会更新。每个 epoch一次,动力学模型 $M_\phi$ 会更新以提高其准确性。如果需要,表示编码器 $\sigma$ 也可以在此时更新,研究发现每5个epoch重新训练一次 $\sigma$ 就足够了。
深度学习架构
尽管上一节中的动力学模型 $M_\phi$ 和编码器 $\sigma$ 可以通过任何合适的方法参数化,但本文发现使用深度神经网络对两者进行参数化在雅达利游戏基准测试中取得了良好的实证结果。
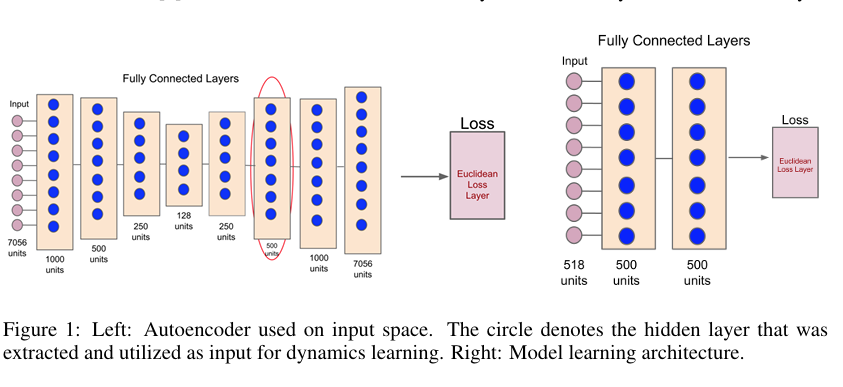
编码器建模
本文选择自动编码器作为编码器的模型,并比较了两种图像捕获和自动编码器训练的方法:
- 静态自动编码器 (Static AE): 随机智能体运行足够长的时间来收集所需图像。自动编码器 $\sigma$ 在策略学习算法开始之前离线训练。
- 动态自动编码器 (Dynamic AE): 使用ε-贪婪策略初始化,并在智能体在策略学习算法下运行时收集图像和动作。在5个 epoch 后,从这些数据中训练自动编码器。继续收集数据并定期与策略训练算法并行地重新训练自动编码器。
自动编码器的第六层的输出(在上图中用圆圈表示)随后被用作状态空间的编码。
动力学模型建模
$M_\phi$ 采用一个两层神经网络建模。$M_\phi$ 将状态 $s_t$ 在时间 $t$ 的编码版本以及智能体的动作 $a_t$ 作为输入,并试图预测下一个帧的编码 $\sigma(s_{t+1})$。损失通过欧几里得损失层计算,回归到真实值 $\sigma(s_{t+1})$。