原文链接：Unifying Count-Based Exploration and Intrinsic Motivation

简介

主流的探索方法包括两类：基于计数的探索（count-based exploration）和内在动机（intrinsic motivation）。前者有坚实的理论基础但难以扩展到高维空间，后者更灵活但理论保障不足。这篇论文提出了一种优雅的桥梁：伪计数（pseudo-count），一种从任意密度模型（density model）中推导出的“伪访问次数”指标，使得基于计数的方法可以泛化到非表格（non-tabular）和高维空间。

方法

状态相关定义

状态空间：用可数集 $\mathcal{X}$ 表示所有可能的状态（例如Atari游戏中的每一帧画面）。
状态序列：长度为 $n$ 的状态序列记为 $x_{1:n} \in \mathcal{X}^n$，
状态序列集合：所有有限序列的集合记为 $\mathcal{X}^*$，即$\mathcal{X}^*=\bigcup_{n=0}^\infty\mathcal{X}^n$
$x_{1:n}x$ 表示在序列 $x_{1:n}$ 后追加一个状态 $x$，空序列记为 $\epsilon$。
这些符号后面要用到，在这里统一定义。

经验分布

一般用$r(x)=r_i(x)+\mathcal{B}(\hat{N}(x))$表示智能体获得的奖励，其中$r_i{(x)}$是环境提供的奖励，$\mathcal{B}(\hat{N}(x))$则衡量了状态的不确定程度。例如在UCB算法中，$\mathcal{B}(\hat{N}(x))=\sqrt{\frac{2lnT}{\hat{N}(x)}}$。本文则选择了一个变种，$\mathcal{B}(\hat{N}(x))=\sqrt{\frac{1}{\hat{N}(x)}}$。那么接下来的问题是，${\hat{N}(x)}$如何计算。
对于表格状态空间，可以用经验分布（Empirical Distribution）来计算。从序列 $x_{1:n}$ 中计算的经验分布 $\mu_n(x)$ 是状态 $x$ 出现的频率：

$$ \mu_n(x) := \frac{N_n(x)}{n}, \quad \text{其中} \quad N_n(x) := \text{状态} x \text{在} x_{1:n} \text{中出现的次数。} $$

但是对于连续状态空间，如图像，经验分布无法计算，因为$N_n(x)\approx0$。于是本文引入密度模型以及伪计数的概念，通过伪计数对连续状态空间的状态进行统计。

从密度模型到伪计数

密度模型（Density Model）是一个映射 $\rho: \mathcal{X}^* \to \text{概率分布}$。根据这个定义，经验分布事实上是一个特殊的密度模型。
对于任意序列 $x_{1:n}$，密度模型输出一个概率分布 $\rho_n(x) := \rho(x ; x_{1:n})$，表示在观察到 $x_{1:n}$ 后，下一个状态是 $x$ 的概率，即在当前状态序列下某状态出现的概率，这个概率也可以用一个频率来逼近：

$$\rho_{n}(x)=\frac{\hat{N}_{n}(x)}{\hat{n}}$$

其中$\hat{N}_{n}(x)$定义为状态$x$的伪计数（Pseudo-Count），$\hat{n}$ 为总状态数的伪计数。那么伪计数可以如何根据密度模型计算呢？

重编码概率与伪计数计算

定义状态$x$的重编码概率(Recoding Probability)：

$$\rho_{n}'(x):=\rho\left(x ; x_{1: n} x\right)$$

这是密度模型在观察到$x$的新出现后为$x$分配的新概率。

在观察到一个$x$的实例后，密度模型对同一$x$的预测增加量应对应于伪计数的单位增加量：

$$\rho_{n}'(x)=\frac{\hat{N}_{n}(x)+1}{\hat{n}+1}$$

联立

$$\rho_{n}(x)=\frac{\hat{N}_{n}(x)}{\hat{n}}$$

可得：

$$\hat{N}_{n}(x)=\frac{\rho_{n}(x)\left(1-\rho_{n}'(x)\right)}{\rho_{n}'(x)-\rho_{n}(x)}$$

这种构造满足：当密度模型为经验分布时，伪计数退化为真实访问次数。

对密度函数的要求

现在的问题是，什么样的模型可以作为密度函数。首先，思考密度函数应该满足的性质：

由于$\hat{N}_n(x) \geq 0$，因此$\rho$ 应满足学习正向 (Learning-Positive) ，即 $\rho_n'(x) \geq \rho_n(x)$
当从未见过 $x$时，即 $\hat{N}_n(x) = 0$时，要求 $\rho_n(x) = 0$。
当已经见到过非常多次的状态，即 $\hat{N}_n(x) = \infty$时，要求 $\rho_n(x) = \rho_n'(x)$。
本文选择了CTS模型。

在Freeway环境中的应用

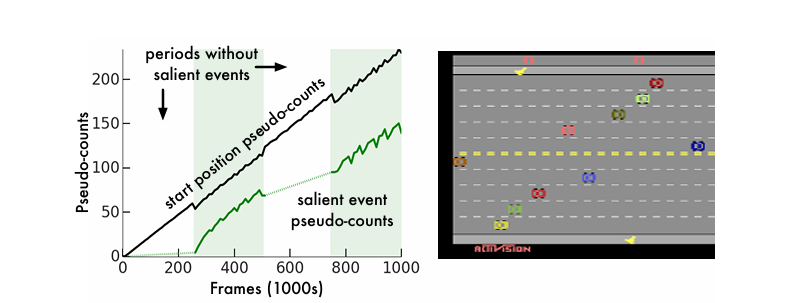
在Freeway游戏环境，游戏任务是控制一只小鸡过马路，在过马路的过程中可能会被小车撞击导致倒退。小鸡被初始化在马路的一边，目标是控制小鸡到达马路对边。左侧曲线横轴代表和环境交互的步数，纵轴代表伪计数。黑色曲线代表小鸡初始化的位置对应的伪计数、变化趋势是持续正向增加，和真实发生的次数的变化趋势一致。绿色曲线代表小鸡到达马路对面对应的伪计数，淡绿色区域对应的时间段内，小鸡到达了马路对面，伪计数变化趋势是迅速增加，而在小鸡还没有到达过马路对面时，其伪计数接近于0。

理论分析

与内在动机的联系

信息增益与预测增益的关系

信息增益（Information Gain, IG）通常用于量化“新颖性”，定义为观察状态后先验与后验分布的KL散度，反映模型对状态的认知变化。
预测增益（Prediction Gain, PG）是另一种度量，定义为状态重新编码前后的对数概率差，即 $$PG_n(x) = \log \rho_n'(x) - \log \rho_n(x)$$，其中 $\rho_n'(x)$ 是观察状态后的密度模型预测概率。
关键关系：预测增益可近似信息增益，且当密度模型具有学习正向性时时，预测增益非负。

伪计数与探索奖励的理论优势

定理1指出：$$IG_n(x) \leq PG_n(x) \leq \hat{N}_n(x)^{-1}$$ 且 $$PG_n(x) \leq \hat{N}_n(x)^{-1/2}$$说明基于伪计数的探索奖励（如 $\hat{N}_n(x)^{-1/2}$）是信息增益和预测增益的上界，因此具有更好的探索性。
传统内在动机方法（如基于预测误差的奖励）缺乏理论保证，而伪计数通过与经验计数的关联，保留了表格环境下的理论性质（如PAC-MDP最优性）。

渐近分析（Asymptotic Analysis）

伪计数与经验计数的比率极限

假设1：定义了密度模型的收敛性条件，要求 $\rho_n(x)$ 与经验分布 $\mu_n(x)$ 的比率极限 $r(x)$ 和学习率极限 $\dot{r}(x)$ 存在且 $\dot{r}(x) > 0$。
定理2：在假设1下，伪计数与经验计数的比率极限为 $$\lim_{n\to\infty} \frac{\hat{N}_n(x)}{N_n(x)} = \frac{r(x)}{\dot{r}(x)} \left(\frac{1 - \mu(x)r(x)}{1 - \mu(x)}\right)$$，表明当模型收敛时，伪计数能渐进逼近真实访问计数的比例。
推论1：当密度模型为表格模型（如Dirichlet估计）时，$\hat{N}_n(x)/N_n(x) \to 1$，即伪计数等价于经验计数，验证了方法的一致性。

学习率衰减的要求

若密度模型的学习率不按 $n^{-1}$ 衰减（如按 $n^{-2/3}$ 衰减），则伪计数与经验计数的比率极限可能发散，无法保证有效性。

重要结论

一致性保证：在合理的密度模型假设下，伪计数在长期训练中能渐进匹配真实访问计数的分布，确保探索策略的稳定性。
模型设计指导：强调密度模型的学习率需按 $n^{-1}$ 衰减，否则无法与经验计数有效比较，为非表格环境下的探索算法设计提供了理论约束。

参考

强化学习中的探索与利用（count-based) - 知乎